這學期在學離散數學的代數與集合論，剛好上到了 Stirling 數這一章，老師便叫我們寫個程式來計算 Stirling 數並撰寫實驗報告，要用遞迴和非遞迴方式實現並比較兩者差異，計算公式本來就是遞推，所以用遞迴很好實現，主要是非遞迴的實現思路較為難想，當時其實已經把這篇文章的原型寫好了，最後的時間複雜度比較我想要用圖表來呈現，不過當時案牘勞形沒時間研究繪製方法，擱到了寒假才繼續完成。

概念

Stirling 數是用來計算一個集合中可以分組的組合數量，公式如下，n 是集合中元素數量，k 是組合數，利用遞迴關係可以求出 Stirling 數。

$$S(n, k)=S(n-1, k-1)+k \cdot S(n-1, k)$$

表格遞推法

假設欄數代表公式中的 n，列則是 k，已知當 $n=1$ 和 $n=k$ 時的組合數為 1(n 個元素分 1 組的組合數為 1，且 n 個元素分 n 組的組合數為 1)，由此可遞推更高階的 Stirling 數。

根據上面的遞迴關係式，要求的那格等於欄數乘上一列格子的值再加上左上方格子的數字，假設我要求第 6 列第 3 欄的值，已知要求 $S(6, 3)$，左上角($S(5, 2)$)數字是 15，在加上上面那格 $S(6, 2)$，就可以得到 $15+3\times25=90$。

1 2 3 4 5 6
1 1
2 1 1
3 1 3 1
4 1 7 6 1
5 1 15 25 10 1
6 1 31 90 65 15 1

程式撰寫

假設

我認為遞迴是最簡單快速的方法，因為不用考慮其他複雜邏輯，而非遞迴還需要一個時間複雜度將所有堆疊彈出求和，所以我先假設遞迴的時間應該會比用非遞迴的時間時間短，不過根據我改良的方法時間複雜度應該會大幅下降。

輸入

輸入兩個數字，第一個數字是欄數 $n$，第二個數字是列數 $k$。

使用遞迴

用遞迴來寫是最直覺簡單的方式了，程式碼也較為簡單，遞迴中止的條件設 $k=1$ 和 $n=k$ 時返回 1，核心程式碼如下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

int s(n, k)
{
    if(n == 1 || n == k)
    {
        return 1;
    }
    else
    {
        return s(n-1, k-1)+k*s(n-1, k);
    }
}

非遞迴

一般人可能直覺想到用陣列來畫表格推算，但是這樣時間、空間複雜度會很高，經過我一夜的思考，想到用堆疊(stack)來存儲遞迴的過程，實驗多次總算寫出成品了，先寫個結構來記錄 Stirling 數的參數，n, k 前面解釋過了，而 times 的目的是用來記錄這個 Stirling 數前面的乘數，還記得前面 Stirling 數的遞迴關係式嗎？

$$S(n, k)=S(n-1, k-1)+k \cdot S(n-1, k)$$

times 就是代表 $S(n-1, k)$ 前面的 $k$，預設值為 1。

1
2
3
4
5
6

struct Stirling
{
    int n;
    int k;
    int times;
};

定義兩個堆疊，一個存結構，一個存算出來的值。

1
2

stack<Stirling> s;
stack<int> ans;

先輸入 n, k，並寫入到 Stirling 的結構裡推入推疊中。

1
2
3
4

int n, k;
scanf("%d %d", &n, &k);
Stirling stirling = {n, k, 1};
s.push(stirling);

接下來就是核心部份了，會先從 s 取堆疊頂端，看 n, k 是否符合條件(n==1 || n==k)，如果條件為真就在 ans 推入 times 的值並彈出 s，否則將 s 彈出，聲明兩個 Stirling 型態的結構 new1 和 new2，分別代表公式中的 $S(n-1, k-1)$ 和 $S(n-1, k)$ 並推入堆疊中，這步驟是為了將原本的 $S(n, k)$ 拆分成子問題，當條件符合中就會彈出 s，直到 s 為空迴圈終止，而拆分出來的子問題解答會存在 ans 堆疊中。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

while (!s.empty())
{
    Stirling top, new1, new2;
    top = s.top();
    if (top.n == top.k || top.n == 1)
    {
        ans.push(top.times);
        s.pop();
    }
    else
    {
        new1 = {top.n - 1, top.k - 1, top.times * 1}, new2 = {top.n - 1, top.k, top.times * top.k};
        s.pop();
        s.push(new1);
        s.push(new2);
    }
}

最後將 ans 中的值一個一個彈出求和就是答案了。

1
2
3
4
5
6
7

int sum = 0;
while (!ans.empty())
{
    int a = ans.top();
    sum += a;
    ans.pop();
}

時間比較

我在計算完成後將計算時間寫入到檔案裡，並用 Python + Matplotlib 繪製三維散佈圖表，可視化兩種實現方法的時間差異，初學 Matplotlib 製圖，下面圖片都是直接在 GUI 界面儲存的，如果有更好的方法歡迎告訴我。

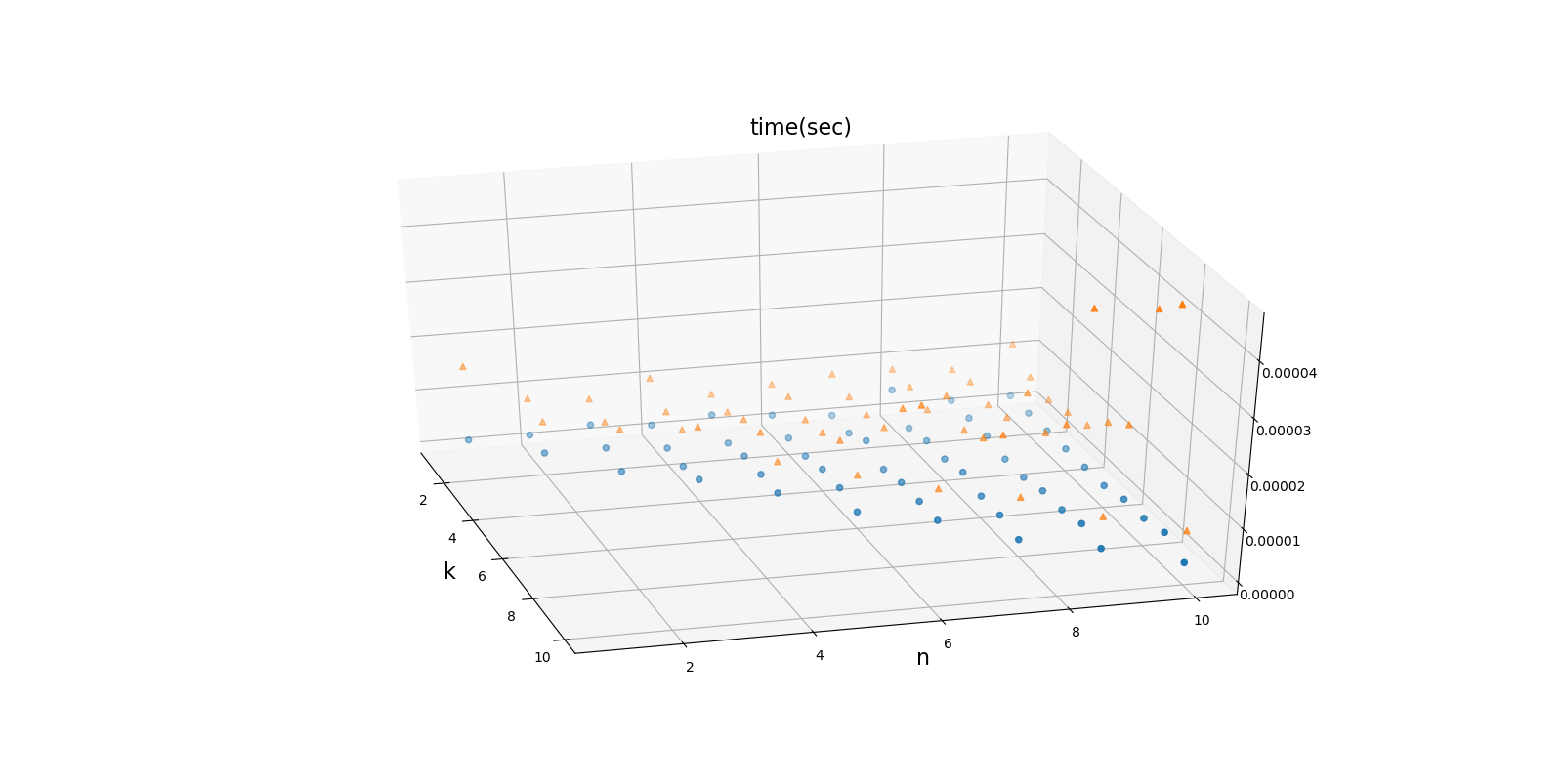
下面是 n 從 1~10 的時間比較，橘色三角形是非遞迴的實現時間，可以明顯看出非遞迴在 $k$ 值愈高的時候所花費的計算時間比遞迴多愈多。

n 從 1~10

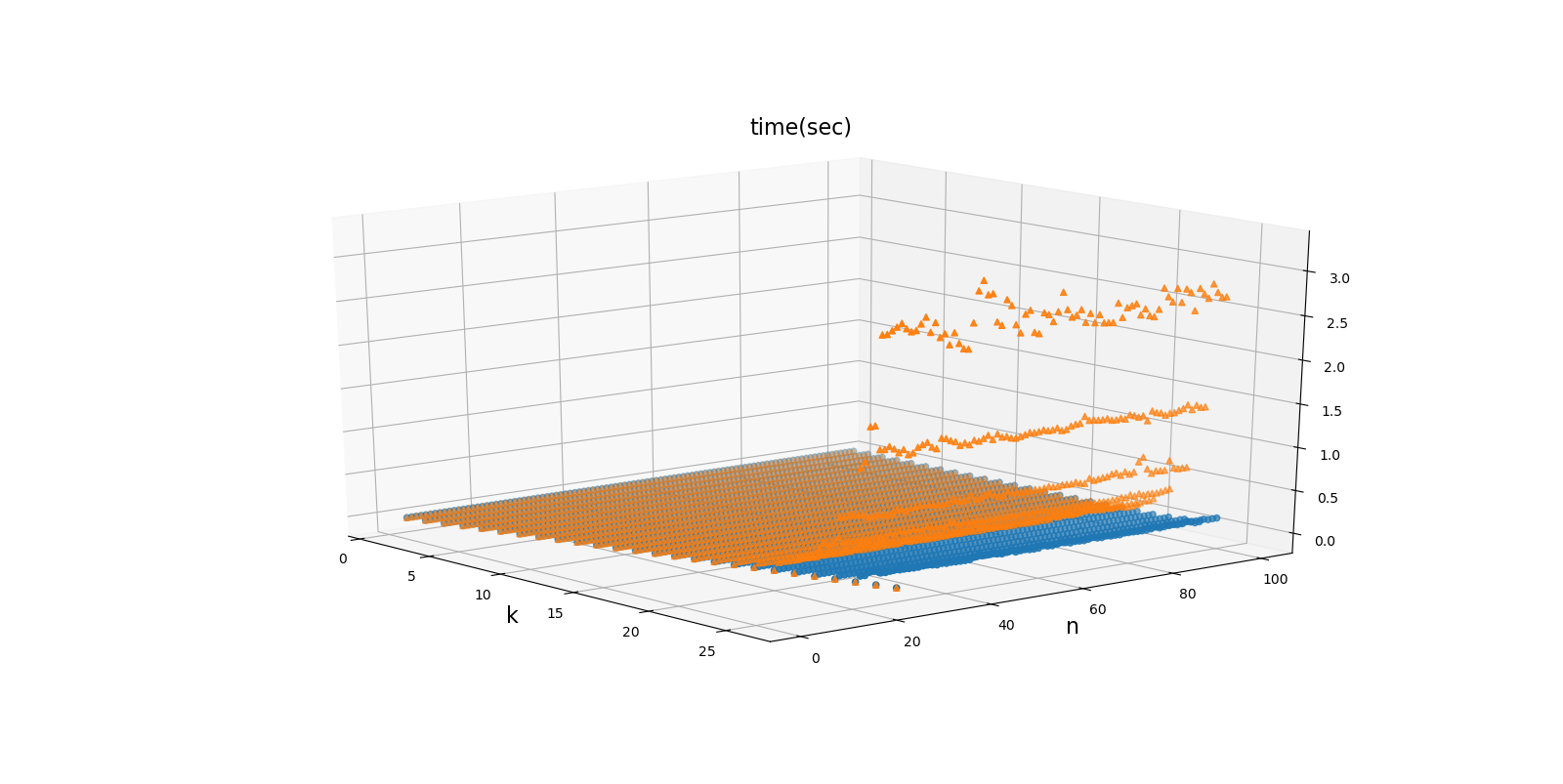
接下來把 $n$ 的範圍加大到 25，其實我本來是想跑到 100 的，但是我發現這樣計算量太大，所以只算到 $n = 25$，這樣差不多有兩千多筆資料，可以看見非遞迴所用時間隨著 k 的變大呈指數型成長。

n 從 1~25

結論

即使我的非遞迴實現採用堆疊去減少時間複雜度和空間複雜度，但還是比不過用遞迴實現的速度，這種遞推公式貌似遞迴做是最快的。